Il s’agit d’une réflexion sur la transmission de puissance entre deux roues dentées afin de faciliter la compréhension de la dynamique de couple.
rmq : travail en cours et non publié donc pouvant comporter des erreurs.
1. Couples
Soit une roue motrice de rayon $R_1$ (rayon du cercle primitif). Celle-ci subit/est le siège d’un certain couple moteur $C_{m1}$, dont l’évolution au cours du temps et de la vitesse de rotation dépend du type de moteur. Supposons que la roue soit dentée et qu’elle est connectée à une autre roue dentée de rayon $R_2$ (« récepteur »). L’accélération de la roue au cours du temps est donnée par (je fais l’hypothèse que le contact ne se fait que via 2 dents) :
\[C_{m1}-f_{T} R_1\cos\alpha-f_{fr} R_1\sin\alpha = J_1 \epsilon_1\]
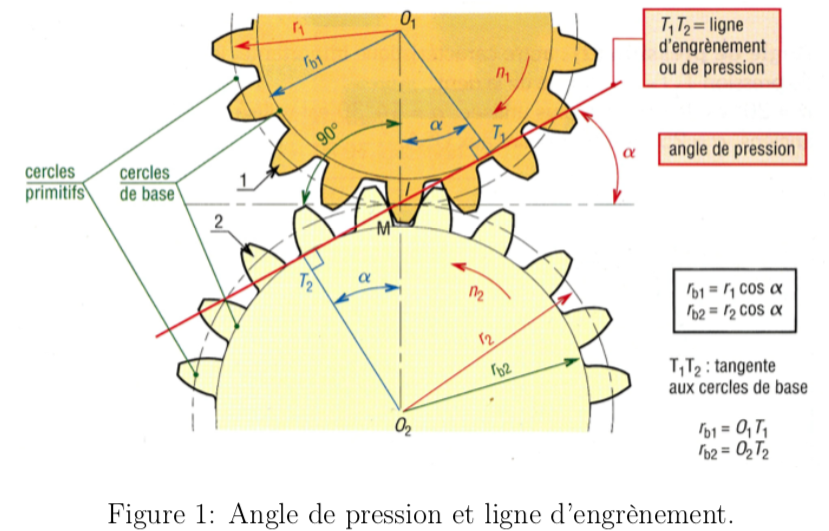
où $f_{T}$ désigne la force de réaction de la roue réceptrice sur la roue motrice, orientée suivant la ligne d’engrènement/de pression, qui forme un angle $\alpha$ avec la tangente aux cercles primitifs. A cause du mouvement relatif entre les dents, une force de frottement $f_{fr}$ existe et génère un couple résistif supplémentaire. J’ai négligé les autres types de frottements mais on pourrait très bien les intégrer dès maintenant (ex. : couple de frottement constant issu de l’axe, couple de frottement issu de l’air, etc.) Dans l’hypothèse des frottements solide-solide on a $f_{fr}=\mu f_{T}$ avec $\mu$ le coefficient de frottement dynamique entre les roues. L’équation ci-dessus devient alors :
\[C_{m1}-f_{T} R_1\left(\cos\alpha+\mu\sin\alpha\right) = J_1 \epsilon_1\]
ce qui paraît cohérent car la réaction de la roue réceptrice sur la roue motrice ainsi que les frottements sont résistifs.
Du côté de roue réceptrice, par action-réaction celle-ci subit des couples issus des forces $f_{T}$ et $f_{fr}$ de sorte que son mouvement est donné par :
\[f’_TR_2\cos\alpha-f’_{fr} R_2\sin\alpha -C_{charge}= J_2 \epsilon_2\]
où $f’_T$ est « moteur » alors que $f’_{fr}$ non. Cette roue peut éventuellement subir un couple résistif supplémentaire $C_{charge}$. Par action réaction $f’_T=f_T$ et $f’_{fr}=f_{fr}$ (on suppose les dents rigide) de sorte que :
\[f_TR_2\left(\cos\alpha-\mu\sin\alpha\right) -C_{charge}= J_2 \epsilon_2\]
Par ailleurs, les accélérations angulaires des deux roues sont reliées via le rapport de transmission (pas de « glissement » car roues dentées) :
\[i=\frac{\omega_1}{\omega_2}=\frac{\epsilon_1}{\epsilon_2}\]
On a donc
\[f_T = \frac{1}{R_2\left(\cos\alpha-\mu\sin\alpha\right)}\left(J_2\epsilon_1/i+C_{charge}\right)\]
Si l’on injecte cette expression dans le mouvement de la roue motrice, on obtient :
\[C_{m1}-\frac{R_1}{R_2}\frac{\left(\cos\alpha+\mu\sin\alpha\right)}{\left(\cos\alpha-\mu\sin\alpha\right)} \left(J_2\epsilon_1/i+C_{charge}\right)= J_1 \epsilon_1\]
Le rapport des rayons est relié au rapport de transmission via $R_1/R_2=1/i$. On peut dès lors réexprimer cette équation :
\[\boxed{C_{m1}=\left[J_1+\left(\frac{\cos\alpha+\mu\sin\alpha}{\cos\alpha-\mu\sin\alpha}\right)\frac{J_2}{i^2}\right]\epsilon_1+\left(\frac{\cos\alpha+\mu\sin\alpha}{\cos\alpha-\mu\sin\alpha}\right)\frac{C_{charge}}{i}}\]
Cette équation met en évidence le concept de moment d’inertie équivalent :
$$J_{eq}\equiv \left[J_1+\left(\frac{\cos\alpha+\mu\sin\alpha}{\cos\alpha-\mu\sin\alpha}\right)\frac{J_2}{i^2}\right]$$
qui dépend de manière quadratique de l’inverse du rapport de transmission et qui dépend de l’angle de pression $\alpha$ et du coefficient de frottement $\mu$. De plus, l’équation met en évidence le changement de couple de charge ressenti au niveau moteur. On peut aussi le voir différemment : $C_{charge}$ est aussi le couple qui peut être fourni par la roue réceptrice.
2. Puissances
En termes de puissances, il suffit de multiplier à gauche et à droite par $\omega_1$
\[C_{m1}\omega_1=\left[J_1+\left(\frac{\cos\alpha+\mu\sin\alpha}{\cos\alpha-\mu\sin\alpha}\right)\frac{J_2}{i^2}\right]\epsilon_1\omega_1+\left(\frac{\cos\alpha+\mu\sin\alpha}{\cos\alpha-\mu\sin\alpha}\right)\frac{C_{charge}}{i}\omega_1\]
car avec $P_{mot}\equiv C_{m1}\omega_1 $ et $P_{ut}\equiv C_{charge}\omega_2=C_{charge}\omega_1/i$ on obtient
\[P_{mot}=\left[J_1+\left(\frac{\cos\alpha+\mu\sin\alpha}{\cos\alpha-\mu\sin\alpha}\right)\frac{J_2}{i^2}\right]\epsilon_1\omega_1+\left(\frac{\cos\alpha+\mu\sin\alpha}{\cos\alpha-\mu\sin\alpha}\right)P_{ut}\]
Cette expression met en avant le fait que la puissance motrice $P_{mot}$ est répartie en puissance nécessaire pour l’accélération (premier terme) et en puissance utile (liée au dernier terme).
Le rendement $\eta\equiv\frac{P_{ut}}{P_{mot}}$ est dès lors donné par :
\[\eta\equiv\frac{P_{ut}}{P_{mot}}= \frac{\cos\alpha-\mu\sin\alpha}{\cos\alpha+\mu\sin\alpha}\left[1-J_{eq}\frac{\epsilon_1\omega_1}{P_{mot}}\right]\]
Avec $P_{mot}=C_{m1}\omega_1$ de sorte que
\[\eta= \frac{\cos\alpha-\mu\sin\alpha}{\cos\alpha+\mu\sin\alpha}\left[1-J_{eq}\frac{\epsilon_1}{C_{m1}}\right]\]
En phase d’accélération, au plus l’accélération angulaire $\epsilon_1$ est grande, au moins le rendement est bon car alors au plus de puissance est utilisée pour l’accélération des roues. En régime nominal, $\epsilon_1=0$ de sorte que
\[\eta^{nom}=\frac{\cos\alpha-\mu\sin\alpha}{\cos\alpha+\mu\sin\alpha}\]
On voit que le rendement est d’autant meilleur que le coefficient de frottement $\mu$ est petit et que l’angle $\alpha$ est petit. Logique. A noter que le moment d’inertie équivalent peut aussi s’exprimer :
\[J_{eq}\equiv \left[J_1+\frac{J_2}{\eta^{nom}i^2}\right]\]
Généralisation des frottements
En termes de puissances, en phase de démarrage, la puissance motrice est répartie en puissance utile, dissipée et « d’accélération ».
\[P_{mot}(t)=P_{acc}(t)+P_{ut}(t)+P_{dissip}(t)\]
Juste après le démarrage, les vitesses sont encore petites de sorte que $P_{dissip}\sim 0$ et $P_{ut}=C_{ut}\omega_{ut}\sim 0$. Toute la puissance est utilisée pour accélérer le système et il reste peu de puissance utile (voir figure ci-dessous). Attention cependant cette phase d’accélération contient de frottements (voir ci-dessus).
En régime nominal la puissance motrice est réparties en puissance utile et en puissance dissipées par les forces de frottement, qui sont alors constant puisque les vitesses sont constantes.
\[P^{nom}_{mot}=P^{nom}_{ut}+P^{nom}_{dissip}\]
Le rendement nominal est alors donné par
\[\eta^{nom}=1-\frac{P^{nom}_{dissip}}{P^{nom}_{mot}}\]
Avec la relation ci-dessus, on a
\[\frac{P^{nom}_{dissip}}{P^{nom}_{mot}}=\frac{2\mu\sin\alpha}{\cos\alpha+\mu\sin\alpha}\]
Le facteur 2 est cohérent avec le fait qu’il y a des frottements sur chacune des 2 roues dentées. En effet :
\[P_{dissip}\equiv \left|\frac{dW_{frott}}{dt}\right| =\sum \left|\vec f_{frott}\cdot \vec v\right|=2\mu f_T v_R\equiv A\omega_1 \]
où $v_R$ désigne la vitesse relative entre les dents qui dépend certainement linéairement de $\omega_1$ qui saute alors dans la fraction ci-dessus -> ok cohérent. L’avantage de cette formulation est qu’il est possible de généraliser à tout type de frottements. En effet, ceux-ci ne sont pas forcément constants et peuvent dépendre de la vitesse, de sorte que (développement en série) :
\[P_{dissip}=\sum \left|\frac{d W_{frot}}{dt}\right|=\sum \left|\vec f_{frot}\cdot\vec v\right|+\left|\vec M_{frot}\cdot\vec \omega\right|=A\, \omega_1+B \, \omega_1^2+C \, \omega_1^3+…\]
A noter que c’est consistant avec les théorèmes :
\[dK_{syst} = \sum \delta W=P_{mot}\, dt+\delta W_{ut}+\sum \delta W_T+\sum \delta W_{frott}\]
où $\sum W_T=0$ désigne le travail des forces de contact, $\delta W_{frott}<0$ (car frottements opposés à la vitesse) et $\delta W_{ut}<0$ (car couple opposé à la vitesse – action/réaction : le système tire et subit)
\[\delta W_{ut}=-P_{mot}\, dt+dK_{syst}-\sum \delta W_{frott}\]
En termes de puissances :
\[P_{ut}= -\frac{dW_{ut}}{dt}= P_{mot}-\frac{dK_{syst}}{dt}+\frac{dW_{frott}}{dt}=P_{mot}-P_{acc}-P_{dissip}\]
où j’ai définit $P_{acc}= dK_{syst}/dt=\sum dK/dt =\sum J\epsilon\omega$ qui est bien en accord avec la forme $J_{eq}\epsilon_1\omega_1$ rencontrée plus haut. Pour trouver le moment d’inertie équivalent « ressenti » par la roue motrice, il suffit donc bien de s’intéresser à l’énergie cinétique :
\[K_{syst}=\sum K=\frac{1}{2}J_{eq} \omega^2_1\]
Attention cependant car cette méthode n’inclut pas la compréhension du rendement dans $J_{eq}$, qui provient des frottements ($P_{dissip}$ ci-dessus).
3. Généralisation
En prenant en compte les couples de frottements supplémentaires sur l’axe, etc. on trouve rapidement :
\[\boxed{C_{m1}=\left[J_1+\frac{J_2}{\eta^{nom}_{dents}i^2}\right]\epsilon_1+\left[C_{frot}^{mot}(\omega_1)+\frac{C_{frot}^{rec}(\omega_1)}{\eta^{nom}_{dents}i}\right]+\frac{C_{charge}}{\eta^{nom}_{dents}i}}\]
où $C_{frot}^{mot}(\omega_1)$ et $C_{frot}^{rec}(\omega_1)$ désignent les couples de frottements supplémentaires sur chacune des roues dentées. Cette expression met en avant de manière simple que le couple moteur est utilisé pour accélérer le système (terme 1), vaincre les couples de frottements issus des axes, de l’air, etc. (terme 2) et fournir un couple utile (terme 3). Attention car le rendement total nominal est maintenant différent d’avant et plus complexe (c’est pourquoi j’ai spécifié $\eta^{nom}_{dents}$). Après développement, je trouve
\[C_{m1}=\left[\frac{\eta^{nom}_{tot}}{\eta^{nom}_{dents}} J_1+\frac{J_2}{\eta^{nom}_{tot}i^2}\right]\epsilon_1+\frac{C_{charge}}{\eta^{nom}_{tot}i}\]
où
\[\eta^{nom}_{tot}=\eta^{nom}_{dents}\left\{1-\left[C_{frot}^{mot}(\omega^{nom}_1)+\frac{C_{frot}^{rec}(\omega^{nom}_1)}{\eta^{nom}_{dents}i}\right]/C_{m1}\right\}\]